알고리즘
1. 시간 복잡도
시간 복잡도(Time Compexity)
- 컴퓨터 프로그램의 입력값과 연산 수행 시간의 상관관계
- 효율적 알고리즘이란?
- 입력값이 커짐에 따라 증가하는 시간의 비율을 최소화한 알고리즘
시간 복잡도의 종류

O(1): 상수 시간 복잡도
✔ ex: 인덱스를 통한 접근
예시 코드
int[] arr = {1, 2, 3, 4, 5};
int x = arr[2]; // retrieves the element at index 2O(N): 선형 시간 복잡도
✔ ex: 일반적인 순회 및 탐색
예시 코드
int[] arr = {5, 3, 8, 1, 7, 2};
int max = Integer.MIN_VALUE;
for (int i = 0; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
System.out.println("Maximum value: " + max);
O(logN): 로그 시간 복잡도
✔ ex: 이분탐색
예시 코드
int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int target = 5;
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (arr[mid] == target) {
System.out.println("Found at index " + mid);
break;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}O(NlogN): 선형 로그 시간 복잡도
✔ ex: 정렬 (퀵 소트, 머지 소트 등)
예시 코드
void quicksort(int[] arr, int left, int right) {
if (left < right) {
int pivotIndex = partition(arr, left, right);
quicksort(arr, left, pivotIndex - 1);
quicksort(arr, pivotIndex + 1, right);
}
}
int partition(int[] arr, int left, int right) {
int pivotValue = arr[right];
int i = left - 1;
for (int j = left; j < right; j++) {
if (arr[j] < pivotValue) {
i++;
swap(arr, i, j);
}
}
swap(arr, i + 1, right);
return i + 1;
}
void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
int[] arr = {5, 3, 8, 1, 7, 2};
quicksort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));O(N^2)
✔ ex: 버블 소트, 이차원 배열 탐색 등등
예시 코드
public static void bubbleSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
boolean swapped = false;
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
swapped = true;
}
}
if (!swapped) {
break;
}
}
}O(2^N): 지수 시간 복잡도
✔ ex: 부분집합 구하기
예시 코드
void generateSubsets(int[] arr) {
int n = arr.length;
int totalSubsets = (int) Math.pow(2, n);
for (int i = 0; i < totalSubsets; i++) {
for (int j = 0; j < n; j++) {
if ((i & (1 << j)) != 0) {
System.out.print(arr[j] + " ");
}
}
System.out.println();
}
}
int[] arr = {1, 2, 3};
generateSubsets(arr);2. 정렬
✔ 실제 cs 질문에는 각 정렬 방식의 개념에 대한 비교와 수도 코드 작성이 나올 수 있으니 잘 알아두자!
버블 정렬 (Bubble Sort)
✔ 인접한 두 원소를 비교하여 정렬하는 알고리즘
✔ 가장 단순하고 직관적이지만 시간 복잡도가 O(N^2)
예시 코드
public static void bubbleSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
선택 정렬 (Selection Sort)
✔ 주어진 배열에서 가장 작은 값을 찾아서 앞으로 가지고 오는 것을 반복하여 정렬하는 알고리즘
✔ 시간 복잡도: O(N^2)
예시 코드
public static void selectionSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
int minIndex = i;
// 주어진 배열에서 최솟값 찾기
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
// 최솟값과 위치 바꿔주기
int temp = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = temp;
}
}삽입 정렬 (Insertion Sort)
✔ 배열의 모든 요소를 앞에 원소들과 비교 하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘
✔ 시간 복잡도: O(N^2)
예시 코드
public static void insertionSort(int[] arr) {
int n = arr.length;
for (int i = 1; i < n; i++) {
int key = target[i];
int j = i - 1;
// 타겟이 이전 원소보다 작으면 이전 원소를 뒤로 한 칸씩 민다
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
// 타겟을 위치에 맞게 삽입해준다
arr[j + 1] = target;
}
}퀵 정렬 (Quick Sort)
✔ 특정한 값(피벗)을 기준으로 큰 숫자와 작은 숫자를 서로 교환한 뒤에 배열을 반으로 분할하여 정렬하는 알고리즘
✔ 분할 정복
✔ 불안정 정렬
✔ O(nlogn) / O(N^2) (최악)
✔ 최악인 경우: 이미 정렬되어있는 배열, 피벗이 최댓값이나 최솟값일 때
- [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
→ 1을 피벗으로 잡고 진행하면 모든 수마다 피벗을 잡고 탐색을 하게 되기 때문에 시간 복잡도가 O(n^2)가 된다!
예시 코드
// 분할 정복 퀵 정렬
public static void quickSort(int[] arr, int low, int high) {
if (low < high) {
int pivotIndex = partition(arr, low, high);
quickSort(arr, low, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, high);
}
}
// 피벗 기준으로 정렬
private static int partition(int[] arr, int low, int high) {
// 중앙 피벗
int mid = low + (high - low) / 2;
int pivot = arr[mid];
int i = low - 1;
int j = high + 1;
while (true) {
// 피벗보다 작은 값
do {
i++;
} while (arr[i] < pivot);
// 피벗 보다 큰 값
do {
j--;
} while (arr[j] > pivot);
if (i >= j) {
// 엇갈린 경우 피벗 교체 후 반환
return j;
}
// 피벗 왼쪽에는 작은 값이, 오른쪽에는 큰 값이 위치하게 된다
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}병합 정렬 (Merge Sort)
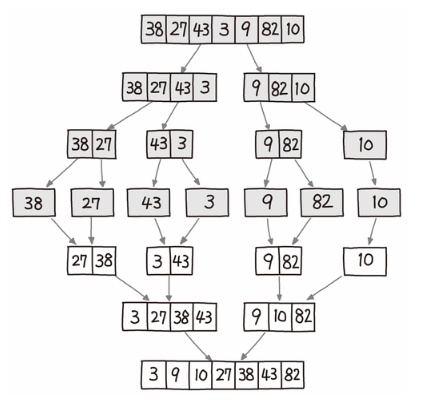
출처: 파이썬 알고리즘 인터뷰
✔ 원소 개수가 0이나 1이 될 때까지 값을 쪼갠 뒤 병합하면서 정렬하는 방법
✔ 시간복잡도: O(logN)
✔ 안정 정렬
✔ 임시 배열을 위한 추가 공간 복잡도
예시 코드
// 분할 정복으로 병합정렬 수행
public static void mergeSort(int[] arr, int low, int high) {
if (low < high) {
int mid = low + (high - low) / 2;
mergeSort(arr, low, mid);
mergeSort(arr, mid + 1, high);
merge(arr, low, mid, high);
}
}
private static void merge(int[] arr, int low, int mid, int high) {
// 배열 분할
int n1 = mid - low + 1;
int n2 = high - mid;
int[] leftArr = new int[n1];
int[] rightArr = new int[n2];
for (int i = 0; i < n1; i++) {
leftArr[i] = arr[low + i];
}
for (int j = 0; j < n2; j++) {
rightArr[j] = arr[mid + j + 1];
}
int i = 0;
int j = 0;
int k = low;
// 분할한 배열 정렬
while (i < n1 && j < n2) {
if (leftArr[i] <= rightArr[j]) {
arr[k] = leftArr[i];
i++;
} else {
arr[k] = rightArr[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = leftArr[i];
i++;
k++;
}
while (j < n2) {
arr[k] = rightArr[j];
j++;
k++;
}
}
각 정렬의 시간 복잡도
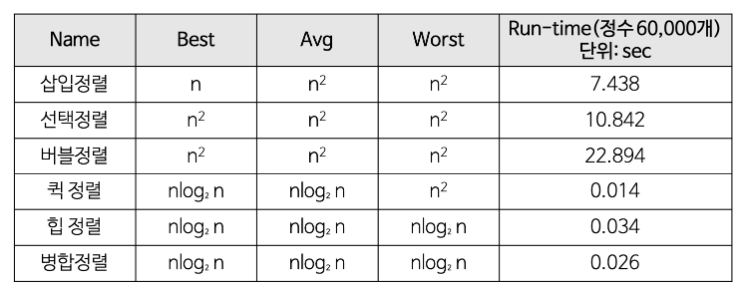
3. 재귀
✔ 함수 내부에서 함수가 자기 자신을 또 다시 호출하여 문제를 해결하는 알고리즘
✔ 반환 / 중단 조건을 잘 설정하는 것이 중요하다!
예시 코드 (팩토리얼 / 피보나치)
// 팩토리얼
public static int factorial(int n) {
if (n == 0) {
return 1;
} else {
return n * factorial(n - 1);
}
}// 피보나치
public static int fibonacci(int n) {
if (n <= 1) {
return n;
} else {
return fibonacci(n - 1) + fibonacci(n - 2);
}
}4. Dynamic Programming
✔ 작은 부분 문제들의 해를 구하고 이를 이용하여 보다 큰 크기의 부분 문제를 해결해 나가며 최종적으로 원래 주어진 문제를 해결하는 알고리즘
✔ DP의 두 가지 조건
- 최적 부분 구조 (Optimal Substructure)
- 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있음
- 중복되는 부분 문제 (Overlapping Subproblem)
- 동일한 작은 문제를 반복적으로 해결해야함
✔ 메모이제이션 (Memoization)
- 한 번 계산한 결과를 메모리 공간에 메모하는 기법
- 다이나믹 프로그래밍을 구현하는 방법 중 하나
- 같은 문제를 다시 호출하면 메모했던 결과를 그대로 가져옴
- 값을 기록해 놓는다는 점에서 캐싱(Caching)이라고도 함
예시 코드 (피보나치)
public static int dpFibonacci(int n) {
if (n <= 1) {
return n;
}
int[] fib = new int[n+1];
fib[0] = 0;
fib[1] = 1;
for (int i = 2; i <= n; i++) {
fib[i] = fib[i-1] + fib[i-2];
}
return fib[n];
}예시 코드 (0/1 knapsack)
// N: 가방 크기, K: 무게
static int knapsack(int N, int K, int[] volume, int[] price){
dp = new int[N + 1][K + 1];
for (int i = 0; i <= N; i++) {
for (int j = 0; j <= K; j++) {
if (i == 0 || j == 0) {
dp[i][j] = 0;
} else if (volume[i - 1] <= j) {
dp[i][j] = Math.max(price[i - 1] + dp[i - 1][j - volume[i - 1]], dp[i - 1][j]);
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[N][K];
}5. 그래프 탐색 / 백트래킹
BFS (Breadth-First Search)
✔ 그래프에서 가까운 노드부터 우선적으로 탐색
✔ 큐(선입선출) 자료 구조 사용
✔ 탐색 과정
- 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
- 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리한다.
- 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.
✔ (모든 간선의 비용이 동일할 떄) 최단 거리를 구하는 데 사용
DFS (Depth-First Search)
✔ 그래프에서 깊은 부분을 우선적으로 탐색
✔ 재귀 / 스택(후입선출) 자료 구조 사용
✔ 탐색 과정
- 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
- 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문 처리를 한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
- 2번 과정을 더 이상 수행할 수 없을 때까지 반복한다.
✔ 백트래킹 / 모든 경우를 하나하나 다 탐색하는 경우 주로 사용
BFS vs DFS
✔ 시간 복잡도는 둘다 O(V + E)로 동일
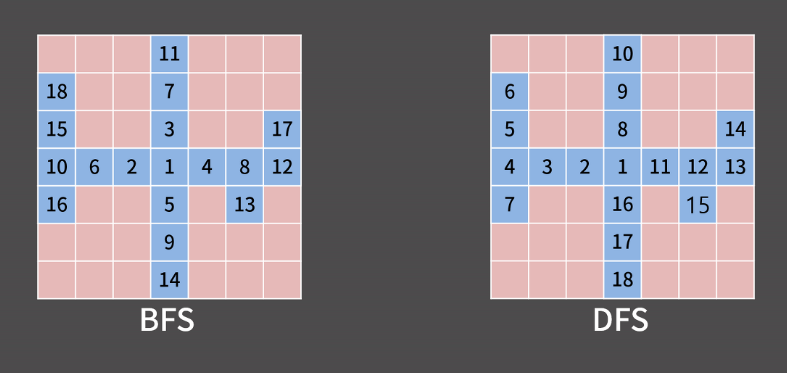
출처: 바킹독 블로그
예시 코드
import java.util.*;
public class Graph {
private int V;
private LinkedList<Integer>[] adj;
// 그래프 구현
public Graph(int v) {
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; i++) {
adj[i] = new LinkedList<>();
}
}
public void addEdge(int v, int w) {
adj[v].add(w);
}
// BFS (큐 사용)
public void bfs(int s) {
boolean[] visited = new boolean[V];
LinkedList<Integer> queue = new LinkedList<>();
visited[s] = true;
queue.add(s);
while (!queue.isEmpty()) {
s = queue.poll();
System.out.print(s + " ");
Iterator<Integer> i = adj[s].listIterator();
while (i.hasNext()) {
int n = i.next();
if (!visited[n]) {
visited[n] = true;
queue.add(n);
}
}
}
}
// DFS (재귀 사용)
public void dfs(int v) {
boolean[] visited = new boolean[V];
dfsUtil(v, visited);
}
private void dfsUtil(int v, boolean[] visited) {
visited[v] = true;
System.out.print(v + " ");
Iterator<Integer> i = adj[v].listIterator();
while (i.hasNext()) {
int n = i.next();
if (!visited[n]) {
dfsUtil(n, visited);
}
}
}
public static void main(String[] args) {
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
System.out.print("BFS traversal starting from vertex 2: ");
g.bfs(2); // "BFS traversal starting from vertex 2: 2 0 3 1"
System.out.print("\nDFS traversal starting from vertex 2: ");
g.dfs(2); // "DFS traversal starting from vertex 2: 2 0 1 3"
}
}
6. 그래프 심화
벨만포드 알고리즘
✔ (가중치가 있는 그래프에서) 한 노드에서 다른 노드까지의 최단 거리를 구하는 알고리즘
✔ (다익스트라와는 다르게) 간선의 가중치가 음수일 때도 사용 가능
✔ 모든 간선을 탐색하면서 인접한 정점에 대한 최단 거리 갱신 (Edge relaxation)
✔ 시간 복잡도: O(VE)
✔ 탐색 과정
- 출발점에서 모든 정점까지의 거리를 저장하는 dist[] 배열을 초기화한다. (dist[start] = 0, dist[v] = 무한대)
- 그래프의 모든 정점 u에 대해, 다음 과정을 V-1번 반복해 수행한다:
- 그래프의 모든 간선(u, v)에 대해, dist[u] + weight(u, v) < dist[v]이면, dist[v]를 새로운, 더 짧은 거리로 갱신한다.
- 그래프에서 음의 가중치 사이클이 있는지 확인한다.(음의 가중치 사이클이 존재할 시 제대로 탐색하지 못한다)
- 출발점에서 모든 정점까지의 최단 거리를 담고 있는 dist[] 배열을 반환합니다.
예시 코드
import java.util.Arrays;
public class BellmanFord {
private int V, E;
private Edge[] edges;
// 그래프 생성자
public BellmanFord(int v, int e) {
V = v;
E = e;
edges = new Edge[e];
}
public void addEdge(int src, int dest, int weight, int i) {
edges[i] = new Edge(src, dest, weight);
}
// 벨만포드 알고리즘
public void bellmanFord(int src) {
// 최소 거리 배열 초기화
int[] dist = new int[V];
Arrays.fill(dist, Integer.MAX_VALUE);
dist[src] = 0;
// 모든 엣지에 대해 최솟값 갱신
for (int i = 1; i < V; i++) {
for (int j = 0; j < E; j++) {
int u = edges[j].src;
int v = edges[j].dest;
int weight = edges[j].weight;
if (dist[u] != Integer.MAX_VALUE && dist[u] + weight < dist[v]) {
dist[v] = dist[u] + weight;
}
}
}
// 음의 가중치 사이클 확인
for (int i = 0; i < E; i++) {
int u = edges[i].src;
int v = edges[i].dest;
int weight = edges[i].weight;
if (dist[u] != Integer.MAX_VALUE && dist[u] + weight < dist[v]) {
System.out.println("Negative weight cycle detected");
return;
}
}
printDistances(src, dist);
}
// 결과값 출력
private void printDistances(int src, int[] dist) {
System.out.println("Shortest distances from source vertex " + src + " to all vertices:");
for (int i = 0; i < V; i++) {
System.out.println("Vertex " + i + ": " + dist[i]);
}
}
public static void main(String[] args) {
int V = 5;
int E = 8;
BellmanFord graph = new BellmanFord(V, E);
graph.addEdge(0, 1, -1, 0);
graph.addEdge(0, 2, 4, 1);
graph.addEdge(1, 2, 3, 2);
graph.addEdge(1, 3, 2, 3);
graph.addEdge(1, 4, 2, 4);
graph.addEdge(3, 2, 5, 5);
graph.addEdge(3, 1, 1, 6);
graph.addEdge(4, 3, -3, 7);
int source = 0;
graph.bellmanFord(source);
// Shortest distances from source vertex 0 to all vertices:
// Vertex 0: 0
// Vertex 1: -1
// Vertex 2: 2
// Vertex 3: -2
// Vertex 4: 1
}
}
// 간선 클래스
class Edge {
int src, dest, weight;
public Edge(int src, int dest, int weight) {
this.src = src;
this.dest = dest;
this.weight = weight;
}
}다익스트라 알고리즘
✔ 음의 가중치가 없는 그래프의 한 정점에서 모든 정점까지의 최단거리를 각각 구하는 알고리즘
✔ 탐색과정
- 출발점으로부터 최단거리를 저장할 배열 distance[v]을 만들고 출발 노드는 0, 나머지 노드들은 충분히 큰 값으로 초기화 한다.
- 현재 노드 Current를 출발 노드의 번호로 설정한다.
- Current로부터 갈 수 있는 임의의 노드 Next에 대해 distance[Current] + P[Current][Next](A를 거쳐서 B로 가는 최단거리)와 distance[Next](현재까지 알려진 B의 최단 거리)의 값을 비교해서 짧은 값(짧은 경로)로 갱신한다.
- Current의 모든 이웃노드 Next에 대해 3 을 수행한다.
- Current의 상태를 ‘visited=True’로 바꿔준다. (Current는 더 이상 사용하지 않는다.)
- visited == False인 노드 중 출발점으로부터 거리가 가장 짧은 노드를 Current로 설정한다.
- 도착 노드가 'visited == True’가 되거나, 더 이상 미방문 노드를 선택할 수 없을 때까지 3 ~ 6의 과정을 반복한다
✔ 시간 복잡도: O(V^2)
✔ 우선순위큐를 이용해 바로 다음 노드에 대한 정보를 추출해내서 최적화 할 수 있다 -> 시간 복잡도 O(ElogE)
예시 코드
import java.util.*;
public class Dijkstra {
private int V;
private List<Edge>[] adj;
// 그래프(인접리스트) 클래스 선언 및 초기화
public Dijkstra(int v) {
V = v;
adj = new ArrayList[v];
for (int i = 0; i < v; i++) {
adj[i] = new ArrayList<>();
}
}
public void addEdge(int src, int dest, int weight) {
adj[src].add(new Edge(dest, weight));
adj[dest].add(new Edge(src, weight));
}
// 다익스트라 알고리즘 (우선순위큐)
public void dijkstra(int src) {
PriorityQueue<Node> pq = new PriorityQueue<>();
// 최단거리 테이블 초기화
int[] dist = new int[V];
Arrays.fill(dist, Integer.MAX_VALUE);
dist[src] = 0;
pq.add(new Node(src, 0));
while (!pq.isEmpty()) {
int u = pq.poll().vertex;
// 우선순위큐 이용해 최단 거리 갱신
for (Edge e : adj[u]) {
int v = e.dest;
int weight = e.weight;
if (dist[u] != Integer.MAX_VALUE && dist[u] + weight < dist[v]) {
dist[v] = dist[u] + weight;
pq.add(new Node(v, dist[v]));
}
}
}
printDistances(src, dist);
}
// 결과값 출력
private void printDistances(int src, int[] dist) {
System.out.println("Shortest distances from source vertex " + src + " to all vertices:");
for (int i = 0; i < V; i++) {
System.out.println("Vertex " + i + ": " + dist[i]);
}
}
public static void main(String[] args) {
int V = 5;
Dijkstra graph = new Dijkstra(V);
graph.addEdge(0, 1, 9);
graph.addEdge(0, 2, 6);
graph.addEdge(0, 3, 5);
graph.addEdge(0, 4, 3);
graph.addEdge(2, 1, 2);
graph.addEdge(2, 3, 4);
int source = 0;
graph.dijkstra(source);
// Shortest distances from source vertex 0 to all vertices:
// Vertex 0: 0
// Vertex 1: 7
// Vertex 2: 6
// Vertex 3: 5
// Vertex 4: 3
}
}
// 엣지랑 노드 클래스 정의
class Edge {
int dest, weight;
public Edge(int dest, int weight) {
this.dest = dest;
this.weight = weight;
}
}
class Node implements Comparable<Node> {
int vertex, dist;
public Node(int vertex, int dist) {
this.vertex = vertex;
this.dist = dist;
}
public int compareTo(Node other) {
return Integer.compare(dist, other.dist);
}
}7. 최소 신장 트리 (Minimum Spanning Tree)
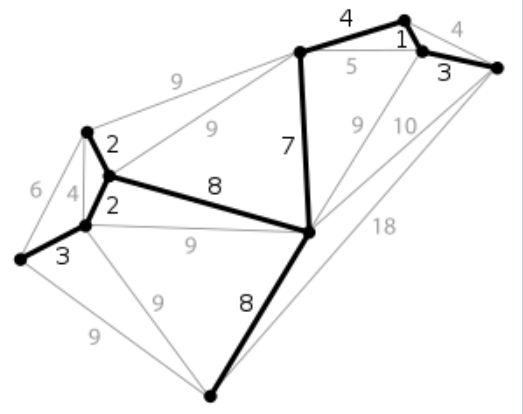
✔ 신장트리: 그래프 내의 모든 정점을 포함하는 트리
✔ 최소 신장트리 Spanning Tree 중에서 간선의 가중치 합이 최소(Minimun)인 트리
구현: 크루스칼 알고리즘
✔ Greedy를 이용해 각 단계에서 사이클을 이루지 않는 최소 비용 간선을 선택한다.
✔ 탐색 과정
- 간선을 오름차순으로 정렬한다. (최소 비용)
- 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택한다. (유니온 파인드)
- 선택한 간선을 현재 MST집합에 추가한다
예시 코드
import java.util.*;
public class KruskalMST {
private int V, E;
private List<Edge> edges;
// 그래프 선언 및 초기화
public KruskalMST(int v, int e) {
V = v;
E = e;
edges = new ArrayList<>();
}
public void addEdge(int src, int dest, int weight) {
edges.add(new Edge(src, dest, weight));
}
public int kruskalMST() {
// parent 배열 초기화
int cost = 0;
int[] parent = new int[V];
Arrays.fill(parent, -1);
// 최소 신장 트리 갱신
for (Edge e : edges) {
// 사이클 판별
int root1 = find(parent, e.src);
int root2 = find(parent, e.dest);
if (root1 != root2) {
// 비용 계산
cost += e.weight;
// 유니온
parent[root1] = root2;
}
}
return cost;
}
// 파인드 함수(사이클 판별)
private int find(int[] parent, int v) {
if (parent[v] < 0) {
return v;
}
parent[v] = find(parent, parent[v]);
return parent[v];
}
public static void main(String[] args) {
int V = 5;
int E = 7;
KruskalMST graph = new KruskalMST(V, E);
graph.addEdge(0, 1, 2);
graph.addEdge(0, 3, 6);
graph.addEdge(1, 2, 3);
graph.addEdge(1, 3, 8);
graph.addEdge(1, 4, 5);
graph.addEdge(2, 4, 7);
graph.addEdge(3, 4, 9);
int cost = graph.kruskalMST();
System.out.println("Total cost of the Minimum Spanning Tree: " + cost);
// Total cost of the Minimum Spanning Tree: 16
}
}
// 간선 클래스 정의
class Edge implements Comparable<Edge> {
int src, dest, weight;
public Edge(int src, int dest, int weight) {
this.src = src;
this.dest = dest;
this.weight = weight;
}
public int compareTo(Edge other) {
return Integer.compare(weight, other.weight);
}
}
8. 분할정복 / 이분탐색
분할정복
✔ 문제를 나눌 수 없을 때까지 나누어서 각각을 풀면서 다시 합병하여 문제의 답을 얻는 알고리즘
✔ 주로 재귀 활용
✔ 예시: 병합정렬, 퀵정렬, 이분탐색...
분할정복 vs DP
✔ 분할 정복은 분할된 하위 문제가 동일하게 중복이 일어나지 않는 경우에 쓰며, 동일한 중복이 일어나면 동적 프로그래밍을 활용(메모이제이션)
이분탐색 (Binary Search)
✔ (주로 정렬된 데이터에서) 검색 범위를 반으로 줄여 나가면서 검색 값을 찾는 알고리즘
✔ 매개변수 탐색(Parametric search)에서 활용 가능!
✔ 시간 복잡도: O(logN)
예시 코드
public class BinarySearch {
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
public static void main(String[] args) {
int[] arr = {1, 3, 5, 7, 9};
int target = 7;
int index = binarySearch(arr, target);
if (index == -1) {
System.out.println("Target not found in array");
} else {
System.out.println("Target found at index " + index);
}
}
}9. 그리디
✔ 여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달하는 알고리즘
✔ 그리디의 두 가지 조건
- 탐욕스런 선택 조건(greedy choice property)과
- 앞의 선택이 이후의 선택에 영향을 주지 않는다
- 최적 부분 구조 조건(optimal substructure)
- 문제에 대한 최적해가 부분문제에 대해서도 역시 최적해이다.
예시 코드 (냅색)
import java.util.Arrays;
public class FractionalKnapsack {
// 그리디로 배낭 채워넣기
public static double getMaximumValue(int[] weights, int[] values, int capacity) {
int n = weights.length;
double[] ratios = new double[n]; // 가치/무게 비율
// 비율 구하기
for (int i = 0; i < n; i++) {
ratios[i] = (double) values[i] / weights[i];
}
// 물건 정보
Item[] items = new Item[n];
for (int i = 0; i < n; i++) {
items[i] = new Item(weights[i], values[i], ratios[i]);
}
// 정렬
Arrays.sort(items);
double maximumValue = 0;
// 그리디하게 물건 채워 넣기
for (int i = n - 1; i >= 0; i--) {
if (capacity == 0) {
break;
}
double weightToAdd = Math.min(items[i].getWeight(), capacity);
maximumValue += weightToAdd * items[i].getRatio();
capacity -= weightToAdd;
}
return maximumValue;
}
public static void main(String[] args) {
int[] weights = {10, 20, 30};
int[] values = {60, 100, 120};
int capacity = 50;
double maximumValue = getMaximumValue(weights, values, capacity);
System.out.println("Maximum value we can obtain = " + maximumValue); // prints "Maximum value we can obtain = 240.0"
}
}
// 클래스 정의
class Item implements Comparable<Item> {
private int weight;
private int value;
private double ratio;
public Item(int weight, int value, double ratio) {
this.weight = weight;
this.value = value;
this.ratio = ratio;
}
public int getWeight() {
return weight;
}
public int getValue() {
return value;
}
public double getRatio() {
return ratio;
}
@Override
public int compareTo(Item item) {
return Double.compare(this.ratio, item.ratio);
}
}
'⭐ Personal_Study > CS' 카테고리의 다른 글
| CS 면접 질문 정리 - 운영체제 2 (0) | 2023.03.03 |
|---|---|
| CS 면접 질문 정리 - 운영체제 1 (3) | 2023.03.02 |
| CS 면접 질문 정리 - 네트워크 (0) | 2023.02.23 |
| CS 면접 질문 정리 - 자료구조 (0) | 2023.02.12 |
| CS 면접 질문 정리 - 프로그래밍 일반 (0) | 2023.02.06 |
댓글